Tension And Release

Tonal Instruments

Most conventional tonal instruments, when excited, will exhibit a pattern of harmonics in the frequency domain that changes over time. Various instruments will have differing harmonics present, and the decays of those harmonics over time may vary. Consider for example, the sound of a grand piano:

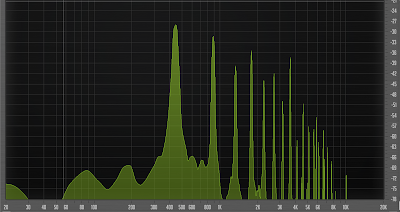
An instantaneous snapshot of the associated spectrum for this audio looks like the following:

Inspection of the each of the peaks in the Spectrum Analyzer used (Voxengo SPAN) reveals that starting with the fundamental (leftmost) peak, the frequencies present in this sound include 442Hz, 884Hz, 1326Hz, 1.78kHz, 2.24kHz, 3.16kHz, 3.62Khz - there were several more harmonics beyond that but those described are sufficient. 

Each of these peaks is a multiple of the fundamental frequency, 442Hz. We can observe that 884Hz is twice 442Hz, 1326Hz is thrice 442Hz etc. 

As we approach the higher harmonics, we note that there is a slight error and these frequencies are not perfect multiples of the harmonic - this is most likely due to the limited precision of SPAN, particular around higher frequencies (it is hard to determine exactly where those higher peaks are).

The fact that these harmonics all occur in multiples of each other is no coincidence - if this was not the case, the sound perceived would unlikely be tonal, or at the very least it would no longer sound like a grand piano. Most tonal instruments will exhibit a very similar harmonic pattern, although which harmonics are stronger and how quickly they decay will vary from instrument to instrument. These differences are what account for the timbre of a particular instrument - this is what gives a guitar playing a note a certain character whereas the same note perceived on a piano will have a different character. 

What is of interest to us is what happens when we stack notes on a piano into chords - Western music theory tells us that within a scale, certain note combinations will be "pleasing" whereas others will be "displeasing". Consider the following two examples:

The average listener would likely consider the first of these examples to be more "pleasing". The reason this is so is because the harmonic relationship between the two notes played - A4 and E5 have respective frequencies: 440Hz and 660Hz. The ratio of these two frequencies is mathematically quite simple, it is 2:3. 

In the latter example we hear A4 and A#4: these correspond to 440Hz and ~466Hz - at best we can simplify this ratio to 220:233. 

We should note that this harmonic relationship generalizes across all of the upper harmonics present in the grand piano note we analyzed previously. In A4 for example, the second harmonic was determined to be ~880Hz, i.e. twice 440Hz. If an E5 note played on a grand piano, the second harmonic can be observed to be 1320Hz, which is twice 660Hz, and the ratio of 880:1320 is also 2:3. For the purpose of this post, we will focus on the relationship between the fundamental frequencies only, and assume that a similar relationship can be inferred for all of the upper harmonics. 

If we were to plot two sinusoids with frequencies 440 and 660 and zoom in on the smallest possible cycle of repetition, we would find that our pattern repeats every 2 oscillations of the slower oscillating wave (440):

This is not the case if we plot 440 and 466Hz sinusoids - we would be hard pressed to find the cycle of repetition visually. Such a repetition occurs every 220 cycles of the 440Hz wave, and correspondingly has 233 cycles of the 466Hz wave: 

We can correlate tonal "stability" with the ratio of frequencies between two tonal sources. For simple ratios, such as 2:3, the tones will superimpose in such a way that frequently repeats, and to the listener seems pleasant. For more complex ratios, such as 220:233, the cycle of repetition is extremely long, and when the two notes are added together the resulting sound comes off as displeasing.  

The important takeaway then is that in order to achieve tension, we want our music to evolve in such a way where the stability lessens over time (complex harmonic ratios), and in order to achieve resolution we want to return to a stable musical idea (simple harmonic ratios). On a grand piano we are somewhat limited to the 12-notes in an octave, but as we shall see electronic music allows us to exploit this idea in interesting ways. 

Fine Tuning & Vibrato

For the remainder of this post, I will be using Serum to synthesize my examples. I will describe how the examples are synthesized, however I will forego any instructional screenshots or videos, as I believe these concepts can be readily applied in a synth-agnostic fashion to most modern digital synthesizers. 

In the previous section we established that tension arises when there is a frequency disparity between notes which cannot be reduced to a simple ratio. Whereas in the previous section we considered this through the lens of multiple notes played simultaneously, here we will explore how we can achieve something similar by modulating the note over time. 

In the classical Western scale, we have 12 notes at our disposal - these will correlate to 12 distinct frequencies. However, between successive notes, there are a number of frequencies that are not covered by any of the notes in the octave. The notes A4 and A#4 correspond to 440Hz and 466Hz - this means 16Hz is unaccounted for between these two notes. 

Some instruments are capable of vibrato, a technique for regular, pulsating variation in pitch. From our perspective, what this means is that the instrument will oscillate in such a way that the frequency of the fundamental moves up and down over time. For example, we can imagine an A4 note that is played in such a way that the emitted fundamental changes over time to cover a range of ±5Hz, thus at any instantaneous point in time the emitted tone is anywhere between 435-445Hz. 

If we consider this in conjunction with the insights from the previous section, we will find that many of these frequencies in a range close to the fundamental do not simplify elegantly, and so many of these will sound tense. As we glide between these frequencies the listener is once again presented with a sense of tension. This example shows the same note played twice, the first time it is a simple sinusoid without any vibrato, the second time the pitch is modulated subtly over time:

With electronic music, we can exploit this effect in interesting ways. Here we play the same note, however as time progresses the vibrato becomes more intense, and fluctuates over a greater range of frequencies:

While this sounds interesting, it does not perhaps convey the same sense of unease as the dissonant tones of adjacent notes on the piano. We can, however, increase the perceived tension by playing from two voices, one of them a stable sinusoid while the other vibrating around it: 

In order to return to a state of resolution, we would simply need to reduce the vibrato. I've found this technique extremely useful for creating risers and ambiences leading into some sort of event, either a new instrument or a break.

We can achieve a very similar effect using Unison, if it is available. Unison will play a central frequency as well as copies of that frequency (Serum supports up to 16 copies) - the location of those copies is determined by a Spread parameter. If this parameter is configured to a low setting, all of the frequencies will sit fairly close to each other. As the Spread is increased, the additional voices are projected to various part of the frequency spectrum. For example, with the voices set to 5, playing the A4 note may result in the frequencies 430Hz, 435Hz, 440Hz, 445Hz, and 450Hz being played. These do not reduce elegantly and so will sound dissonant - it is trivial to modulate the Spread to increase over time, once again creating a riser that mounts tension over time. This can be made increasingly dramatic by increasing the number of voices, though for more complex sounds this may quickly devolve into noise:

Frequency Shifting

Throughout this section, I will be using Ableton's Frequency Shifter - Ableton is my DAW of choice so I shall leave it up to the reader to find a comparable tool for their own workflow. 

The Frequency Shifter is divided into two sections, LFO and Frequency. The LFO section allows you to configure a frequency modulation over time that is determined by the value in the Amount setting. A setting of 20Hz will modulate a sinusoid of 440Hz over the range 420-460Hz. The resulting sound sounds like this:

While this is an interesting sound, it doesn't seem like we've innovated beyond the possibilities of fine-tuning described in the previous section. However, there is a critical difference between fine-tuning and frequency shifting. In the former, the harmonic relationship between the fundamental and the upper harmonics is preserved, whereas in frequency shifting, this relationship is destroyed.

Consider a tone consisting of A4 and its first two harmonics i.e. 440Hz, 880Hz, 1320Hz. It sounds like this:

Adjusting the fine tuning may result in a sound comprised of 420Hz, 840Hz (twice 440Hz), and 1260Hz (thrice 440Hz). However, the same adjustment made in a frequency shifter would result in a sound comprised of 420Hz, 860Hz, 1300Hz - all of the initial frequencies reduced by 20Hz. Note that in the case of the latter, the resulting sound contains harmonics which do not reduce simply. This happens because the frequency axis is logarithmic, but the frequency shift operation is applied on the axis linearly - as a result, the harmonicity between the fundamental and the upper harmonics is not preserved. Applying an LFO with Amount 20Hz to the sound above results in the following:

Because of how the frequency shifter works, aggressive settings can quickly devolve into noise, or other unexpected sounds. However, when applied gently we can exploit the devolution of harmonicity to create tension. We can mimic the sound achieved by Unison described in the previous section with a rack that resembles the following:

A central sound is preserved in the DRY SOUND channel while the FREQ SHIFT channel projects copies of that sound to neighboring frequencies. The resulting sound sounds like this:

The perceived effect is quite similar to the Unison in the previous section, but importantly note that the behavior will be different for each of the harmonics, and so more aggressive settings can be exploited in ways different from Unison.

As a final example, consider the following sound where the Frequency is perturbed by -10Hz and an additional 7Hz is compounded in the LFO section. The sound is then washed in reverb. As the sound evolves, the Dry/Wet of the Frequency Shifter is reduced to 0, returning the harmonics to a stable state and bringing about a sense of resolution:

Conclusion

Any tool that allows you to manipulate the output frequency of a sound (fine tuning, frequency shifting, MIDI arrangement) can be leveraged as a tool to introduce tension to your sounds / arrangements. 

Hopefully this post has provided a deeper understanding of why that is the case. I hope these techniques are helpful and you can leverage some of these principles in creative ways in your own productions.